Memahami Akar Kuadrat: Konsep Dasar & Berbagai Metode Pencariannya

Poltekkes Palembang – Akar kuadrat merupakan salah satu konsep fundamental dalam matematika yang sering ditemui dalam berbagai perhitungan dan aplikasi. Secara sederhana, akar kuadrat dari suatu bilangan adalah nilai yang jika dikalikan dengan dirinya sendiri akan menghasilkan bilangan tersebut. Misalnya, akar kuadrat dari 9 adalah 3, karena 3 dikalikan 3 sama dengan 9. Konsep ini juga dikenal sebagai akar pangkat dua. Dalam notasi matematika, akar kuadrat dilambangkan dengan simbol radikal (√).

Bilangan yang memiliki akar kuadrat berupa bilangan bulat disebut bilangan kuadrat sempurna, seperti 1, 4, 9, 16, 25, dan seterusnya. Namun, tidak semua bilangan memiliki akar kuadrat yang merupakan bilangan bulat; banyak di antaranya menghasilkan bilangan irasional atau desimal tak berulang. Memahami cara mencari akar kuadrat, baik secara manual maupun menggunakan metode lain, sangat penting dalam pelajaran matematika, mulai dari tingkat dasar hingga menengah.

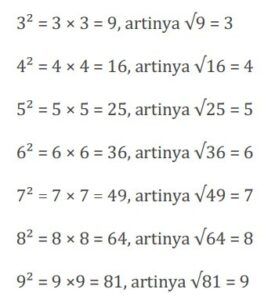
Sejarah dan Pentingnya Akar Kuadrat

Konsep akar kuadrat telah dikenal sejak peradaban kuno. Bangsa Babilonia, misalnya, telah memiliki tabel akar kuadrat dan menggunakan aproksimasi untuk menghitungnya. Dalam konteks modern, akar kuadrat tidak hanya digunakan dalam matematika murni, tetapi juga dalam fisika, teknik, keuangan, dan ilmu komputer. Misalnya, dalam geometri, akar kuadrat digunakan untuk menghitung panjang sisi miring segitiga siku-siku berdasarkan Teorema Pythagoras. Dalam statistika, akar kuadrat digunakan dalam perhitungan standar deviasi.

Metode Pencarian Akar Kuadrat

Ada beberapa metode yang dapat digunakan untuk mencari akar kuadrat suatu bilangan, mulai dari yang sederhana hingga yang lebih kompleks, tergantung pada jenis bilangannya dan tingkat presisi yang dibutuhkan.

1. Metode Faktorisasi Prima

Metode ini efektif untuk mencari akar kuadrat dari bilangan kuadrat sempurna. Langkah-langkahnya adalah sebagai berikut:

• Faktorkan bilangan yang dicari akar kuadratnya menjadi faktor-faktor prima.
• Kelompokkan faktor-faktor prima yang sama menjadi pasangan-pasangan.
• Ambil satu faktor dari setiap pasangan.
• Kalikan faktor-faktor yang telah diambil tersebut. Hasil perkaliannya adalah akar kuadrat dari bilangan awal.

Contoh: Mencari akar kuadrat dari 36.

• Faktorisasi prima dari 36 adalah 2 × 2 × 3 × 3.
• Kelompokkan: (2 × 2) × (3 × 3).
• Ambil satu dari setiap pasangan: 2 × 3.
• Hasilnya adalah 6. Jadi, √36 = 6.

2. Metode Estimasi atau Tebakan

Metode ini cocok untuk bilangan yang tidak terlalu besar dan dapat dilakukan dengan mencoba-coba perkalian bilangan bulat.

• Perkirakan bilangan bulat yang jika dikuadratkan mendekati bilangan yang dicari akar kuadratnya.
• Lakukan percobaan dengan bilangan bulat di sekitar perkiraan tersebut hingga menemukan nilai yang tepat atau mendekati.

Contoh: Mencari akar kuadrat dari 81.

• Kita tahu 9 × 9 = 81. Jadi, √81 = 9.

Metode ini juga dapat dikembangkan dengan melakukan estimasi untuk akar kuadrat yang bukan bilangan bulat. Misalnya, untuk mencari √10, kita tahu 3² = 9 dan 4² = 16. Jadi, √10 berada di antara 3 dan 4. Kita bisa mencoba 3,1² = 9,61, 3,2² = 10,24, dan seterusnya.

3. Metode Pengurangan Berulang (untuk Bilangan Kuadrat Sempurna)

Metode ini didasarkan pada fakta bahwa jumlah n bilangan ganjil pertama adalah n².

• Kurangi bilangan awal dengan bilangan ganjil secara berurutan (1, 3, 5, 7, dst.) hingga hasilnya nol.
• Hitung berapa kali pengurangan dilakukan. Jumlah pengurangan adalah akar kuadratnya.

Contoh: Mencari akar kuadrat dari 25.

• 25 – 1 = 24 (1x)
• 24 – 3 = 21 (2x)
• 21 – 5 = 16 (3x)
• 16 – 7 = 9 (4x)
• 9 – 9 = 0 (5x)
  Pengurangan dilakukan sebanyak 5 kali. Jadi, √25 = 5.

4. Metode Pembagian atau Algoritma Manual

Metode ini lebih sistematis dan dapat digunakan untuk mencari akar kuadrat dari bilangan apa pun, termasuk yang tidak sempurna, hingga beberapa angka desimal. Metode ini mirip dengan pembagian bersusun.

• Pisahkan angka-angka dalam bilangan menjadi pasangan dari kanan ke kiri. Jika ada angka tersisa di paling kiri, biarkan sebagai satu digit.
• Cari bilangan bulat terbesar yang kuadratnya kurang dari atau sama dengan pasangan angka pertama (atau digit pertama). Tulis bilangan ini sebagai digit pertama hasil akar kuadrat.
• Kurangkan kuadrat bilangan ini dari pasangan angka pertama.
• Turunkan pasangan angka berikutnya.
• Gandakan hasil akar kuadrat yang sudah didapat, lalu tambahkan sebuah digit kosong di belakangnya.
• Cari digit yang, jika ditempatkan di digit kosong tersebut dan kemudian dikalikan dengan seluruh angka yang terbentuk, hasilnya kurang dari atau sama dengan sisa angka yang ada. Tulis digit ini di samping hasil akar kuadrat.
• Ulangi langkah-langkah di atas hingga mendapatkan presisi yang diinginkan.

Contoh: Mencari √625.

• Pisahkan: 6 | 25
• Cari bilangan yang kuadratnya ≤ 6, yaitu 2 (2² = 4). Tulis 2 sebagai hasil pertama. Sisa: 6 – 4 = 2.
• Turunkan 25, jadi 225. Gandakan hasil (2) menjadi 4, tambahkan digit kosong (4_).
• Cari _ sehingga 4_ × _ ≤ 225. Jika _ = 5, maka 45 × 5 = 225. Tulis 5 sebagai hasil berikutnya.
• Hasilnya adalah 25.

5. Menggunakan Kalkulator atau Perangkat Lunak

Dalam praktik sehari-hari, terutama untuk bilangan besar atau kebutuhan presisi tinggi, penggunaan kalkulator atau perangkat lunak seperti Microsoft Excel (menggunakan fungsi SQRT) adalah cara yang paling cepat dan mudah. Namun, memahami metode manual tetap penting untuk membangun pemahaman konsep yang kuat.

Akar Pangkat Lainnya

Selain akar kuadrat (pangkat 2), dalam matematika juga dikenal akar pangkat tiga (kubik), akar pangkat empat, dan seterusnya. Akar pangkat tiga dari suatu bilangan adalah nilai yang jika dikalikan dengan dirinya sendiri sebanyak tiga kali akan menghasilkan bilangan tersebut. Misalnya, akar pangkat tiga dari 8 adalah 2, karena 2 × 2 × 2 = 8. Metode pencarian akar pangkat tiga juga memiliki kemiripan dengan akar kuadrat, namun dengan penyesuaian pada prosesnya.

Akar-akar Persamaan Kuadrat

Konsep akar juga meluas pada penyelesaian persamaan kuadrat, yaitu persamaan polinomial berderajat dua yang umumnya berbentuk ax² + bx + c = 0, di mana a ≠ 0. “Akar-akar” dalam konteks ini merujuk pada nilai-nilai x yang memenuhi persamaan tersebut. Ada beberapa metode untuk mencari akar-akar persamaan kuadrat:

1. Faktorisasi

Metode ini melibatkan penguraian persamaan kuadrat menjadi perkalian dua faktor linear.

2. Melengkapkan Kuadrat Sempurna

Metode ini mengubah bentuk persamaan kuadrat menjadi bentuk kuadrat sempurna yang lebih mudah diselesaikan.

3. Rumus ABC (Rumus Kuadratik)

Rumus ABC adalah metode universal yang selalu dapat digunakan untuk mencari akar-akar persamaan kuadrat, bahkan jika faktorisasi sulit dilakukan. Rumusnya adalah:
x₁,₂ = [-b ± √(b² – 4ac)] / 2a
Nilai di bawah akar, yaitu (b² – 4ac), disebut diskriminan (D). Diskriminan menentukan jenis akar-akar persamaan:

• Jika D > 0, ada dua akar real dan berbeda.
• Jika D = 0, ada dua akar real yang kembar (sama).
• Jika D < 0, tidak ada akar real (akar imajiner).

Penerapan dalam Kehidupan Sehari-hari

Meskipun terlihat abstrak, konsep akar kuadrat memiliki banyak aplikasi praktis. Dalam konstruksi, perhitungan akar kuadrat digunakan untuk memastikan sudut dan dimensi yang tepat. Dalam bidang keuangan, akar kuadrat dapat muncul dalam formula yang berkaitan dengan volatilitas investasi. Bahkan dalam seni dan desain, rasio yang melibatkan akar kuadrat dapat ditemukan dalam proporsi estetika.

Dengan berbagai metode yang tersedia, dari perhitungan manual hingga penggunaan teknologi, mencari akar kuadrat dan memahami konsepnya menjadi lebih mudah diakses. Penguasaan konsep ini tidak hanya meningkatkan kemampuan berhitung, tetapi juga membuka pintu untuk pemahaman yang lebih mendalam tentang berbagai fenomena dalam ilmu pengetahuan dan kehidupan sehari-hari.